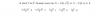Sweex

מישהו\י? :\

היי. זאת גם שאלה מהמועד א' האחרון. פה אני פחות או יותר מבין מה מבקשים ממני למצוא אני פשוט לא מוצא דרך איך למצוא את זה. אפשר עזרה בבקשה?

שאלה מהמועד א' האחרון. יוצא לי 4\1 כי קבעתי שהתחום של Y הוא בין 0 ל- 0.5 ושל X בין 0 ל- 1 כאשר הצפיפות המשותפת של X ו- Y היא 2\1 (כי זה שטח של המשולש). איך מגיעים ל- 3\1? וחבל שלא יכולתי לשאול אתכם במועד א' :-P

הבנתי. כרגיל, תודה רבה :)

העובדה שהם בת"ל ושאפשר להגדיר משתנה לחיסור שלהם נובעת מקונבולוציה?

מצטער להמשיך להציק עם שאלות, אבל הסתברות ח' לצערי לא מקצוע פשוט. בכל מקרה בשאלה הזאת, אני לא מצליח להבין איך אני בכלל מחפש את הווריאנס. אני יכול למצוא את הצפיפות המשותפת של X ו -Y ולנסות דרך ההסתברות למצוא משהו, אבל אני לא יכול לבצע אינטגרציה כי יש לי פה רכיבים שאי אפשר לפרק (X^2 , Y^2) איך אני בכלל ניגש לשאלה הזאת?

כרגיל, תודה רבה :-)

אז מבחינה פורמלית זה יראה ככה? E[N]= 1 +X*P(Y = 1)+ Y*(P(X = 1) ddd כאשר 1 הוא למעשה 1 * 1 הסתברות כי בוודאות תהיה זריקה ראשונה. X משתנה גיאומטרי שסופר עד להצלחה בהסתברות של 3\1 וההסתברות שכופלים בו היא שאני אשתמש בו שהיא 3\2. Y משתנה גיאומטרי שסופר עד לכישלון (בתור הצלחה) עם פרמטר 3\2 וההסתברות שהוא יהיה בשימוש היא 3\1 (במידה ותהיה הצלחה). זה מדוייק לרשום את זה ככה?

אם זה בסדר יש לי עוד שאלה. בשאלה הזאת איך שהלכתי זה הגדרתי שני משתנים גיאומטריים X ו- Y אחד זה מספר הניסויים עד להצלחה והשני עד לכישלון (שמבחינת הניסויים זה מוגדר "כהצלחה"). כלומר X-Geo(1\3)ddd ו- Y-Geo(2\3)ddd. עכשיו צריך לחשב את התוחלת של שני המשתנים ואני חישבתי את הסכום שלהם, אבל אני מודע שיש פה בעיה X ו -Y אינם בת"ל. איך אני אמור להמשיך מהנקודה הזאת? או שיש דרך יותר טובה למצוא את זה?

מלך! תודה! (כשחישבתי את Z שכחתי להשתמש בנוסחא של איחוד מאורעות שזה ההסתברות של A + ההסתברות של B פחות החיתוך שלהם. בגלל זה טעיתי)

יש מצב שאתה מראה את החישוב איך הגעת ל- 6\1? לפי איך שאני מחשב את זה יוצא לי ש- Z מתפלג בצורה אחידה בין 0 לרבע :\

זה

אני לא רוצה להציף נושאים בפורום אז ברשותך עוד שאלה: בשאלה הזאת הלכתי לפי ההדרכה שלהם, מצאתי את פונקציית הצפיפות של A ו- B ששתיהן מתפלגות בצורה אחידה בין 4\1 ל- 0. מכיוון שמבקשים את תוחלת של המינימום של A, B והם משתנים בלתי תלויים אז התוחלת של המינימום של שניהם אמור להיות סכום התוחלות של A ו- B , לא ככה?

אהההה... איזו טעות מפגרת, שכחתי לחלוטין שהם בלתי תלויים אך ורק בתנאי שהם נתונים ביחס ל- X (צלע ריבוע) קבוע. תודה רבה!

זה לא אמור לשנות כי בסופו של דבר הביטוי שנשאר הוא EQyEQx זאת בשל העובדה שהתוחלת המותנית של כל Q היא אמצע הקטע 0 עד X שזה X\2. אז יצא לי שהמומנט השני של X יתבטל יחד עם הביטויים E(XQ) ל- X ו- Y. כנראה שטעיתי אפשהו בהנחה כי אני לא רואה שטעיתי בחישוב :\

אוקיי, עם 4 הסדרתי. אפשר רק עזרה ב- 5?

בקשר לשתי השאלות, אני רוצה להבין מה לא עשיתי נכון כי התשובה שקיבלתי לא תואמת לתשובות: 4. התוחלת של X בהינתן שX>=1 היא הסכום האינסופי של ההתפלגות הפואסנית הנתונה כפול אינדס רץ k , כלומר: E=sum(k=1 to inf)k*e^-1*1\k! E=e^-1*sum(k=1 to inf)1(\k-1)! ddd E=e^-1*e=1 מה לא עשיתי פה נכון? 5. אני הגדרתי את השטח של המלבן הקטן בתור : S=(X-Qx)(X-Qy)=X^2-X*Qy-X*Qx-QxQy ddd ויצאתי מהנחה דיי טבעית שהוקטור Q מתפלג בצורה אחידה כאשר הרכיב X שלו מתפלג בצורה אחידה בין 0 ל - X והרכיב Y שלו מתפלג באותו אופן. מפה הוצאתי תוחלת על S והשתמשתי קצת במשפט ההחלקה ובסופו של דבר יצא לי : 1 חלקי 4 כפול למבדא בריבוע שגם את התשובה הזאת אין. מה לא עשיתי נכון בשני המקרים ? :\

אהה.. שכחתי לגמרי שאפשר לחשב את הסכום הזה תודה !

מה זאת אומרת? הרי הפונקציית התפלגות של משתנה אקראי דיסקרטי מנוסחת כ- P(Y<=y) ddd שזה למעשה הסכום מ- 0 עד y כלשהו (כי זה איחוד מאורעות Y=1 Y=2 Y=3 .... Y=y). פשוט התכוונתי סכום אינסופי כי סופרים מ- K עד אינסוף כאשר ההסתברות ש- X>K.

אוקיי, אבל אפילו ככה. מדובר פה על סכום של כל ההצלחות שקרו אחרי איזה K כלשהו וזה סכום מה- K הזה עד לאינסוף. למה התעלמו מהסכום הזה?

אוקיי, אני פשוט לא מצליח להבין מה עשו בשאלה הזאת כמצאו את פונקציית התתפלגות ל- min(X,Y) ddd. קודם כל למה הם מחשבים את הפונקציה המשלימה של פונקציית ההתפלגות של המינימום. ודבר שני, אם X ו- Y הם כמות ההתלות הדרושות לקבלת הצלחה אז למה אין פה סכום? יותר קריטי בקשר לסכום. הרי איך שאני עושה את זה בד"כ זה מוצא את פונקציית ההתפלגות של המינימום וקורא לה בשם Z למשתנה min(X,Y) ddd. שזה אנלוגי ל- Z גדול מ- X "או" (איחוד מאורעות) Z גדול מ- Y פחות החיתוך. המאורעות בלתי תלויים לחלוטין ולכן החיתוך הוא כפל הסכום של ההסתברויות עד איזה Z. במקרה הזה זה כמובן מסובך מידי כי יוצא לי סכום עד Z בריבוע, אבל למה איך שהם עשו את זה נכון? אני כל פעם רואה את השאלות האלה וכל פעם מסתבך עם ההגדרה של המינימום או המקסימום. אשמח אם מישהו יוכל להבהיר לי את הנקודה הזאת.

ניסיתי, הסתכלתי על השאלה הזאת כמה וכמה פעמים ובאמת אני לא מצליח להבין מה הם רוצים. למה בכלל נתונה לי ההתפלגות של X? עזרה בבקשה

זה אמור להיות X קטן שווה ל- x קטן. לא זאת הנקודה, השאלה שלי למה הם משתמשים בחלק X>0 של פונקציית ההתפלגות כאשר ההתפלגות כמו שרשמת היא עד 0 (x<0). ז"א זה אמור להיות ce^-x.

בשאלה הזאת את C ו- a מצאתי ללא שום בעיות, אבל לא ממש הבנתי למה פונקציית ההתפלגות עד 0 (Fx(0)) הם משתמשים בהתפלגות של X>0 ולא של X<0?

אוקיי לא משנה. אפשר למחוק.