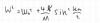Sweex

השאלה היא כזאת. בהרצאה הראו לנו פתרון פאזורי למשוואת גלים א"מ (בתלת מימד כמובן) וגם הראו לנו כי ניתן לבטא את הפתרון בעזרת התמרת פורייה למרחב התדר. עכשיו, היחס נפיצה יוצא אותו הדבר (בהנחה שאנחנו בריק) ואני פשוט תוהה מתי גישה אחת לפתרון עדיפה על השנייה? כמו כן, הצורה הסופית בשני המקרים היא לפלסיאן של השדה החשמלי (או מגנטי) שווה למינוס מספר הגל בריבוע כפול השדה חשמלי\מגנטי. ורשום בהערה כי זה תקף כל עוד לא משתמשים בפולסים קצרים בזמן ו\או חלשים. למה? אלו לא פולסים שניתן לבטא בעזרת הדלתא של דיראק?

זהו, ככה חשבתי על זה גם הבעיה שהיא לא ממש הבנתי מה זה אומר ביחס הנפיצה שהוא בסה"כ משוואה פיזיקלית. עכשיו אבל זה דיי מובן. תודה :-)

נכון. אבל לפי הסיכומים בהרצאות הראו לנו שקיימת דעיכה מדומה של המס' גל. ובגלל שנתנו פתרון בצורה פאזורית של גל מתקדם אז החלק המדומה של המס' גל יורד. הבעיה היא שאני לא מבין למה לעשות את זה בכלל ומה המשמעות הפיזיקילית כאשר האופן תנועה המינימלי הוא כאשר w=g/l... לא מבין את זה.

אומגה. זה כאשר אומגה קטן מאומגה 0. מתקבל אז arctan של מס' מדומה

זה היחס כאשר אומגה 0 זה g/l (אורך החוט , אבל אני מניח שכבר הבנת את זה P:)

כן, זה פשוט ניסוח לא טוב בהרצאה של המשתנים Ka זה המס' גל K זה קבוע הקפיץ. סליחה שלא רשמתי את זה קודם

היי. בהרצאות הראו לנו דוגמה של מערכת של מטוטלות מצומדות בעזרת קפיצים שיחס הנפיצה שלהם הוא לא ליניארי מהצורה: w^2=g/l-(4K/M)*(sin(Ka/2)))^2ddd. עכשיו הראו לנו ניתוח של הפונקצייה מ- 0 עד pi (שזה הכל טוב ויפה) וגם כאשר w קטן מ- sqrt(g/l)ddd והראו לנו כי החל מנקודה זאת יש דעיכה במס' הגל עד אשר w=0... עכשיו מה זה אומר? האופסט של יחס הנפיצה הוא מנקודה g/l , אם אני הופך את היחס כך ש- ka הוא הפונקציה ו- w הוא האינטיג'ר יתקבל לי בהינתן ש- w קטן מ- sqrt(g/l)ddd יתקבל לי arcsin של איזה מס' מרוכב. איך זה בדיוק מראה על דעיכה? למה שאני בכלל אתייחס לתדרים האלה עם המוד הנמוך ביותר הוא התדר sqrt(g/l)ddd

אוקיי לא משנה כבר. זה כל- כך פשוט שזה כבר מטומטם ... זה פשוט הצבה, כאשר p=o אז גם אין שום שינוי ב- x...

אוקיי לא משנה כבר. זה כל- כך פשוט שזה כבר מטומטם ... זה פשוט הצבה, כאשר p=o אז גם אין שום שינוי ב- x...

שאלה עקרונית. נגיד בסעיף א' בשאלה הזאת, נתון לי ההמילטוניאן של חלקיק חופשי. כשאני משתמש במשוואות המילטון רואים שיש שינוי בקצב של p/m בציר x ואין שינוי בציר p לכן הגובה של של המלבן S נשמר. בפתרון שראיתי יש הזזה רק בקודקודים העליונים של (נקודות C ו- D) אבל אני לא מבין למה אין הזזה של כל המלבן במישור הפאזה. זה בגלל שנקודות A ו - B הן תנאי שפה? זה נראה לי הגיוני אבל אני לא לחלוטין סגור.

LOL ידעתי שזה משהו מפגר ופשוט וסתם אני מסתבך עם זוויות. תודה !

יותר עזרה בטריגנומטריה למען האמת, קצת הסבכתי עם הזוויות. איך אני מגיע לתיאור הזה של R? אני לא ממש הבנתי פה ואמנם זה קצת עצוב שאני מסתבך במשהו יחסית פשוט עדיין אשמח מאוד להסבר.

אה, הבנתי. למרות שלא השתכנעתי ב- 100% לגבי הגזירה ב- a של ה- L שווה ל- 0 אבל זה נשמע לי מספיק הגיוני ואין לי באמת כוח למצוא הוכחה מתמטית לזה. בכל מקרה, תודה רבה

זאת כנראה שאלה טריוואלית, אבל זה קטע שטיפה מציק לי. כאשר גוזרים את הלגרנג'יאן בדיספלסיה הוירטואלית a מקבלים 0 ואז גם טוענים שסכום הנגזות החלקיות של הלגרנג'יאן ב- Qjים גם שווה 0. למה? זה בגלל הצורה של הפוטנציאל שהוא פוטנציאל בין חלקיקים? או שזה נכון תמיד? למה גם הגזירה של L ב- a שווה ל- 0?

אה, איך יכולתי לשכוח את חוק שימור החוט! אבל אני חושב שהבנתי למה משתמשים באנרגיה הפוטניאלית. אני רוצה לדעת את צורת החוט והדרך הכי טובה לעשות את זה להשתמש בצורה שיש לה את הפעולה המינימלית. אז אני מגדיר את אוך החוט כפעולה ומשם בעזרת E-L אפשר בסופו של דבר להגיע לצורה.

אני לא רוצה להציף את הפורום בשאלות אז אשאל את זה פה . זה תרגיל מתרגול, ויכול להיות שאני טמבל אבל לא ממש הבנתי בו שני דברים: 1. למה מוצאים את המינימום של האנרגיה הפוטנציאלית ולא נגיד של הלגרנג'יאן? 2. למה קיים אילוץ שאורך החוט יהיה קבוע? מאינטואיציה אני יכול להבין למה זה נכון אבל כבר למדתי לא להסתמך על האינטואיציה שלי בפיסיקה. אשמח מאוד לעזרה.

עשיתי וגם קיבלתי ציון טוב, אבל זה היה לפני שנה וחצי :) קצת שכחתי את החומר ואין לי מחברת חדו"א 2. תודה גדולה על העזרה!

אני מצטער שאני מציק, אבל תוכל בבקשה גם להסביר את המעבר מהמכפלה הוקטורית לביטוי בשורש? ז"א, הסבר לגבי למה אני מבצע את המכפלה כדי למצוא אלמנט של שטח הפנים.

אז איך אני אמור לבטא את האינטגרל הפעולה של שטח הפנים ? לא ממש מצליח להבין במקרה הזה. זה אנאלוגי למקרה הדו מימדי שבו אני מבצע אינטגרל הפעולה הוא אינטגרציה לגבי ציר ה- X של y' +1 בשורש. אז במקרה הזה יהיה לי אינטגרציה כפולה על טטה ו- Z? ואני מגדיר למעשה את הפעולה ככה? Sqrt(dz^2+dr^2)ddd? כי אני דיי בטוח שחסר לי משהו.

האמת זה יותר לכיוון החדו"א 2 וזה משהו שאני קצת לא בטוח איך לפתור. בסעיף 1 אני צריך למצוא ביטוי אינטגרלי לשטח הפנים. עכשיו שטח הפנים כי שהבנתי הוא בעל צורה דומה לשל שעון חול (גם ממה שראיתי מסרטון שמדגים את שטח הפנים של בועת הסבון). יש לי פה צורה שהיא למעשה הרבה עיגולים דו מימדים שמורכבים בפרוסות לאורך Z מ- z0- עד ל- z0 . יוצא שהרדיוס של כל עיגול תלוי באלמנט גובה dz אבל אני לא ממש מצליח לבטא את הרדיוס בתור פונקצייה של z. אשמח לעזרה

זה אומר שפונקציית ההסתברות P(Z=z)dd היא כזאת? 1 מיניס e^-1 אם Z=1 e^-5 כש Z=5 וכל הפונקצייה הזאת חלקי קבוע כלשהו שהוא סכום הקפיצות שיוצא בתכל'ס 1 מינוס e^-1 פלוס e^-5. ופונקציית הצפיפות מוכפלת כפול 1 פחות הקבוע של החלק הבדיד? ניסיתי ככה וסכמתי את ויצא לי תשובה קרובה לזאת שבשאלה אבל לא בדיוק.

היי תודה. אני ניסיתי לעשות את זה דרך פונקציית התפלגות. קבעתי שכאשר X קטן שווה ל- 1 ההתפלגות שווה 0 כש - X בין 1 ל- 5 ההתפלגות היא מעריכית וב- X גדול שווה ל- 5 ההתפלגות היא 1 מה אני עושה מכאן עם פונקציית ההתפלגות הבדידה? יש לי בעיקרון שני קפיצות, אחת מ- 0 ל- 1 מינוס e^-1 ועוד אחת שהיא מההתפלגות הרציפה ל- 1 שזאת קפיצה של 1 מינוס e^-1 פלוס e^-5. אני אמור לרשום את הקפיצות ואז לחלק אותן במשקל הכולל שלהן ? איך זה אמור ללכת?

השאלה הזאת דיי פשוטה, אבל קצת הסבכתי בה. איך אני אמור למצוא את הפונקציות התפלגות והצפיפות האלה?

שאלה נוספת. מקווה שיענו לי. אפשר בבקשה הסבר לגבי הפתרון הזה? אני לא ממש מצליח להבין מה זה ה- Y הזה והדרך שאני ניסיתי לא ממש הולכת לי.

אוקיי לא משנה. הגעתי לתשובה. זה דווקא מאוד פשוט ואני שכחתי לגמרי את הדרך הזאת.