אודי ב

לא מצורף כלום

נתונה מסגרת ריבועית הנושאת זרם אחיד. המומנט המגנטי http://www.codecogs.com/gif.latex?%5Cvec%20m שלה מכוון בכיוון ציר ה-y: http://www.codecogs.com/gif.latex?%5Cvec%20m=m%20%5Chat%20y במרחב יש גם שדה מגנטי המכוון בכיוון ציר ה- http://www.codecogs.com/gif.latex?z: http://www.codecogs.com/gif.latex?%5Cvec%20B=B%20%5Chat%20z ולכן מופעל על המסגרת מומנט כח בכיוון ה -http://www.codecogs.com/gif.latex?x: http://www.codecogs.com/gif.latex?%5Cvec%20N%20=%5Cvec%20m%20%5Ctimes%20%5Cvec%20B=mB%20%5Chat%20x שואלים עכשיו לאן תפנה המסגרת הריבועית בשיווי משקל. כלומר, נניח ומאפשרים לה להגיע לכיוון חופשי, מה יהיה כיוונו של http://www.codecogs.com/gif.latex?%5Cvec%20m בסוף? התשובה היא בכיוון http://www.codecogs.com/gif.latex?-%20%5Cvec%20z ואני לא מבין למה.

נתונה קליפה כדורית הטעונה במטען Q. הקליפה מסתובבת סביב ציר ה z בתידרות זוויתית omega. צריך למצוא את השדה המגנטי במרכז הקליפה. אני רוצה לפתור את השאלה הזו בעזרת הנוסחה הבאה, שמשתמשת בצפיפות הזרם המשטחית: http://www.codecogs.com/gif.latex?B%5Cleft%20(%20%5Cvec%20r%20%5Cright%20)=%5Cfrac%7B%5Cmu_0%7D%7B4%5Cpi%7D%5Cint%20%5Cfrac%7B%5Cvec%20K%5Cleft%20(%20%5Cvec%20r%5E%5Cprime%20%5Cright%20)%5Ctimes(%5Cvec%20r%20-%5Cvec%20r%5E%5Cprime)%7D%7B(%5Cvec%20r%20-%5Cvec%20r%5E%5Cprime)%5E3%7Dda%5E%5Cprime אם ראשית הצירים נמצאת במרכז הקליפה, אז http://www.codecogs.com/gif.latex?%5Cvec%20r=%5Cleft%20(%200,0,0%20%5Cright%20) http://www.codecogs.com/gif.latex?%5Cvec%20r%5E%5Cprime=%5Cleft%20(%20%5Csin%20%5Ctheta%20%5Ccos%20%5Cphi,%5Csin%20%5Ctheta%20%5Csin%20%5Cphi%20,%5Ccos%20%5Ctheta%20%5Cright%20) ו- http://www.codecogs.com/gif.latex?%5Cvec%20K%5Cleft%20(%20%5Cvec%20r%5E%5Cprime%20%5Cright%20)=%5Csigma%5Cleft%20(%5Cvec%20r%5E%5Cprime%20%5Cright%20)%5Cvec%20v%20%5Cleft%20(%20%5Cvec%20r%5E%5Cprime%20%5Cright%20)=%5Csigma%20%5Comega%20R%20%5Csin%20%5Ctheta%5E%5Cprime%20%5Chat%20%5Cphi%5E%5Cprime=%5Csigma%20%5Comega%20R%5Cleft%20(%20-%5Csin%20%5Cphi%5E%5Cprime%20,%5Ccos%20%5Cphi%5E%5Cprime,0%20%5Cright%20) והנוסחה מקבלת את הצורה הבאה: ביצוע המכפלה הוקטורית, ואחר כך חישוב של כל אחד מהרכיבים של האינטגרל אם ידוע כי http://www.codecogs.com/gif.latex?da=R%5E2%20%5Csin%20%5Ctheta%20d%5Ctheta%20d%5Cphi נותן 0 לכל רכיב, שזה לא נכון. התשובה היא http://www.codecogs.com/gif.latex?%5Cvec%20B%5Cleft%20(%200%20%5Cright%20)=%5Cfrac%7B%5Cmu_0%20Q%20%5Comega%7D%7B6%5Cpi%20R%7D%20%5Chat%7B%5Cmathbf%7Bz%7D%7D אני חושב שהטעות שלי נמצאת בבחירה של K. מישהו יכול להצביע על הטעות שלי? ** דרך אגב, ראיתי פתרון לשאלה הזו באמצעות סכימה על השדה של טבעות זרם מה"קוטב" העליון לתחתון. אני מתעקש לפתור את השאלה בדרך שהראיתי כאן עם הביטוי ל-K.

שאלה נוספת אבל דומה: http://i63.tinypic.com/sflcae.png התשובה לסעיף א' היא http://i66.tinypic.com/34ewdbn.png וכאן מופיע עוד פעם החלק שאני לא מבין, בתשובה לסעיף ב': http://i67.tinypic.com/14spci9.png תודה!

תודה על תגובתך אבל, לקחתי את השאלה הזו מספר שאלות-ופתרונות במכניקה ושם מקבלים את התשובה יותר בקלות: השאלה והפיתרון בקבצים המצורפים. אני מתנצל שאני מראה את הפיתרון ואת הניסוח הקצת שונה של השאלה רק עכשיו. בכל מקרה, אשמח אם תעזור לי להבין מה החישוב שנעשה פה ומי הם הגדלים http://www.codecogs.com/gif.latex?%5Clambda,%20%5Cnu%20%5C,%20%5Cmu

יש לי קוביה עם צפיפות הומוגנית בעלת מסה m וארוך צלע a. מהו מומנט האינרציה של הקוביה לסיבוב סביב ציר העובר דרך מרכז הקוביה ומכוון לאחת הפינות? ידוע כי טנזור מומנט האינרציה של הקוביה עבור מערכת צירים הנמצאת במרכזה כשכל אחד מהצירים חותך את הקוביה במרכזי הפאות הוא: http://www.codecogs.com/gif.latex?%5Cfrac%7Bm%20a%5E2%7D%7B6%7D%5Cleft%20(%20%5Cbegin%7Bmatrix%7D הקוביה מסתובבת סביב הוקטור http://www.codecogs.com/gif.latex?%5Cvec%20r%20=%20%5Cfrac%7Ba%7D%7B%5Csqrt3%7D%5Cleft%20(%5Cbegin%7Bmatrix%7D מכיוון שאורך הצלע הוא http://www.codecogs.com/gif.latex?%5Csqrt%7B3%7Da וכתבתי ווקטור יחידה בכיוון הזה. מה השלב הבא שעליי לעשות כדי לחשב את מומנט האינרציה? אני יודע שאני יכול לקבל את וקטור התנע הזוויתי אם אני מכפיל את http://www.codecogs.com/gif.latex?I ב- omega (מכפלת מטריצה בוקטורhttp://www.codecogs.com/gif.latex?%5Comega%20%5Ccdot%20%5Cvec%20r)אבל זה לא מה שמבקשים.

נתון מכיל בצורת גליל כמתואר בציור שנופל ממנו נוזל. צידו העליון של המיכל במגע עם גאז בלחץ P_h. צידו התחתון של המיכל במגע עם האטמופירה. מה הביטוי לגובה הנוזל כתלות בזמן? בפתרון כתוב כך: http://www.codecogs.com/gif.latex?v(z)=const%20%5Cto%20%5CPhi_i=-vz%20%5Cto%20%5Cfrac%7B%5Cpartial%20%5CPhi_i%7D%7B%5Cpartial%20t%7D%20+v%5E2%20/2%20+P/%5Crho%20+%5CPhi_%7Bgrav%7D=f(t) אני לא מבין מאיפה מגיע ההנחה הזו ש v(z) = קבוע. phi_i הוא הפוטנציאל של הזרימה (נוזל אידיאלי בלתי דחיס - קיום זרימה פונציאלית). תודה.

sol1.pdf הנה.

אם אני אומר שנקודות החיתוך של הפירמידה עם הצירים הם ב- dx dy dz ולא ב- a b c אז אתה יכול להסביר את זה? אולי לא הבנתי את הפתרון כמו שצריך, כי לא אמרו את זה במפורש, אני הנחתי שזה כך.

צודק. טעות שלי. מנסים להוכיח את חוק פסקל - הלחץ שמפעיל אלמנט נפח קטן בצורת פירמידה (למשל) של זורם במנוחה זהה בכל הכיוונים בהסתמך על כך שהכוח הפועל על כל משטח ניצב לו. אם אנחנו מדברים על פירמידה כמו שבאיור בהודעה המקורית, אז מכיוון שלחץ הוא כח ליחידת שטח: http://www.codecogs.com/gif.latex?%5Cvec%20p_x=-p_x%20%5Chat%20x,~%5Cvec%20p_y=-p_y%20%5Chat%20y,~%20%5Cvec%20p_z=-p_z%20%5Chat%20z והוקטור של המישור המשופע הוא http://www.codecogs.com/gif.latex?%5Cvec%20p_s=p_s%5Ccdot(a%20%5Chat%20x+b%5Chat%20y+c%5Chat%20z) בשיווי משקל שקול הכוחות הוא אפס ולכן http://www.codecogs.com/gif.latex?%5Cvec%20p_s%20S_s%20+%5Cvec%20p%20_x%20S_x%20+%5Cvec%20p_y%20S_y%20+%5Cvec%20p_z%20S_z=0 ואז הפתרון אומר את מה שכתבתי בהודעה המקורית: http://www.codecogs.com/gif.latex?S_x=a%20S_s,~s_y=bS_s,~S_z=cS_s ופותרים את המשוואה הוקטורית בכל קורדינטה ומקבלים שיוויון בין כל ה- p-ים. יכול להיות שמדלגים על שורה אחת או שתיים? תודה.

נניח ויש לי פירמידה כמתואר באיור. http://i.imgur.com/TU96FU0.png הפתרון של התרגיל אומר כי שטחי הפאות מקיימים: http://www.codecogs.com/gif.latex?%5Cleft%5C%7B%5Cbegin%7Bmatrix%7D כאשר a הוא מיקום הקודקוד של הפירמידה עם ציר x, b עם y c עם z. ו- S_s הוא שטח הפאה שנמצאת בזווית עם מישור xy. מדוע הקשר הנ"ל בין השטחים מתקיים? ניסיתי להראות את זה עם נוסחת Halo לשטח משולש שנתונות 3 הצלעות שלו (מבלי ידע כלשהו על הזוויות), ודי הסתבכתי. תודה.

תודה, אבל אני מדבר על המעבר שלפניו, בין הראשון לשני. מכפילים את http://www.codecogs.com/gif.latex?%5Cpsi_%7B-%7D ב- http://www.codecogs.com/gif.latex?%5Cpsi_%7B+%7D ולכן בגלל שזה כפל של אקסוננטים ולפי חוקי חזקות http://www.codecogs.com/gif.latex?e%5Ea%20%5Ccdot%20e%5Eb%20=e%5E%7Ba+b%7D אז קיבלתי ביטוי שהוא די דומה למה שבתמונה אבל עם + בין ה http://www.codecogs.com/gif.latex?(x-%5Cfrac%7Bl%7D%7B2%7D)%5E2;%20~~(x+%5Cfrac%7Bl%7D%7B2%7D)%5E2. מלבד זה, לאן נעלם http://www.codecogs.com/gif.latex?%5Comega%20t? קיבלתי גם 2kd בתוך האקספוננט (מאותה סיבה של חוקי חזקות). בקיצור קיבלתי את הביטוי הזה מהצבה פשוטה כפי שהסברתי: http://www.codecogs.com/gif.latex?%5Cexp%5Cleft%20%5B%20i%5Cleft%20%5B%202kd+%5Cfrac%7Bk(x-%5Cfrac%7Bl%7D%7B2%7D)%5E2+k(x+%5Cfrac%7Bl%7D%7B2%7D)%5E2%7D%7B2d%7D%20-2%5Comega%20t%20-2%5Cphi-%5Cfrac%7B%5Cpartial%20%5Cphi%7D%7B%5Cpartial%20t%7D%5Cfrac%7B1%7D%7B2dc%7D%5Cleft%20(%20(x-%5Cfrac%7Bl%7D%7B2%7D)%5E2+(x+%5Cfrac%7Bl%7D%7B2%7D)%5E2%20%5Cright%20)%5Cright%20%5D%20%5Cright%20%5D

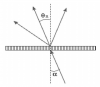
נתון גל מונוכרומטי מישורי בעל מספר גל k התמתקדם בזווית פגיעה alpha לקראת סריג עקיפה מחזורי עם מחזוריות l. אני צריך לחשב את זוויות הקרניים של הלגים המתפזרים מהסריג. כלומר, אני מתייחס לסריג כאל סדרה של מקורות אור נקודתיים עם הפרש פאזה ביניהם שהמרחק ביניהם הוא l. הפאזה היחסית ביניהם נקבעת מהפאזה של הגל הפוגע. אני צריך עזרה במציאת הקשר הזה. הפתרון לתרגיל אומר כי הפרש הפאזה בין שני מקורות סמוכים שממוקמים ב- http://www.codecogs.com/gif.latex?x_j=jl;x_%7Bj+1%7D=(j+1)l הוא http://www.codecogs.com/gif.latex?-kl%20%5Csin(%5Calpha) ואשמח לרמז מדוע זה קורה. בנוסף, מדוע יש "דיסקריטזציה" של http://www.codecogs.com/gif.latex?%5Ctheta_n שרואים בסרטוט? אני בכלל לא מבין מה קורה לקרניים היוצאות מהסריג במקרה הזה של הפרש פאזה כנ"ל. תודה.

אני צריך לחשב את תבנית ההתאבכות של שני מקורות אור נקודתיים הממוקמים במרחק l זה מזה על פני מדך במרחק d המוצב במקביל לקו המחבר בין שני המקורות, המקיים http://www.codecogs.com/gif.latex?d%5Cgg%20%5Cleft%20%7C%20x%5Cpm%5Cfrac%7Bl%7D%7B2%7D%20%5Cright%20%7C. פוקנצית הגל של המקורות: http://www.codecogs.com/gif.latex?%5Cpsi(%5Cvec%20r,%20t)=%5Cfrac%7BA%7D%7Br%7D%5Cexp%5Bi(kr-%5Comega%20t-%20%5Cphi_%7Brand%7D(t-%5Cfrac%7Br%7D%7Bc%7D))%5D phi rand זהה עבור שני המקורות. פיתוח של r לטור טיילור נותן: http://www.codecogs.com/gif.latex?r%5Ccong%20d+%5Cfrac%7B%5Cleft%20(x%5Cpm%5Cfrac%7Bl%7D%7B2%7D%20%5Cright%20)%5E2%7D%7B2d%7D ובהתאם ל- phi: http://www.codecogs.com/gif.latex?%5Cphi%5Cleft%20(%20t-%5Cfrac%7Br%7D%7Bc%7D%20%5Cright%20)%5Ccong%5Cphi%5Cleft%20(%20t-%5Cfrac%7Bd%7D%7Bc%7D%20-%5Cfrac%7B%5Cleft%20(%20x%5Cpm%5Cfrac%7Bl%7D%7B2%7D%20%5Cright%20)%7D%7B2dc%7D%5Cright%20)%5Ccong%5Cphi%5Cleft%20(%20t-%5Cfrac%7Bd%7D%7Bc%7D%20%5Cright%20)-%5Cfrac%7B%5Cpartial%20%5Cphi%20%5Cleft%20(%20t-%5Cfrac%7Bd%7D%7Bc%7D%20%5Cright%20)%7D%7B%5Cpartial%20t%7D%5Cfrac%7B%5Cleft%20(%20x%5Cpm%5Cfrac%7Bl%7D%7B2%7D%20%5Cright%20)%5E2%7D%7B2%20d%20c%7D ה"נוסחה" לעוצמה: http://www.codecogs.com/gif.latex?I(x,t)=%5Cleft%20%5Clangle%20%5Cleft%20%7C%5Cpsi_%7B-%7D%20%5Cright%20%7C%5E2%20%5Cright%20%5Crangle+%5Cleft%20%5Clangle%20%5Cleft%20%7C%5Cpsi_%7B+%7D%20%5Cright%20%7C%5E2%20%5Cright%20%5Crangle+2Re%5Cleft%20%5Clangle%20%5Cpsi_%7B-%7D%5Cpsi%5E*_%7B+%7D%20%5Cright%20%5Crangle ועכשיו, אני לא מבין את הפיתוח לביטוי המעורב. אשמח לעזרה שם (תמונה).

http://www.codecogs.com/gif.latex?(%5Cpartial%20T%20/%20%5Cpartial%20V)_%7BU%7D מה המשמעות של הנגזרת של T ל- V כאשר האנרגיה הפנימית קבועה? עבור גז אידיאלי קיבלתי שזה =0. מה זה אומר עבור גזים אחרים?